Stata provides statistical solutions developed by StataCorp, and it provides programming tools for those who want to develop their own solutions. There are two Stata programming languages: ado, which is easy to use, and Mata, which performs numerical heavy lifting. And Stata is integrated with Python.
Mata’s new Quadrature() class provides adaptive Gaussian quadrature for numerically integrating univariate functions. It approximates the integral from a to b of f(x), where a can be minus infinity or finite and b can be finite or positive infinity.
Quadrature() uses the adaptive Gauss—Kronrod method. It also provides the Simpson method for use in teaching.
LET’S SEE IT WORK
To use Quadrature(), you
define the function to be integrated,
set the lower and upper limits of integration, and
call the Quadrature() to perform the integration.
For instance, imagine we want to integrate the normal density function even though Mata has a built-in cumulative normal. Define the function to calculate f(x) by typing
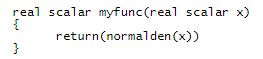
or, if you prefer,

To obtain the integral, you might write

To obtain the integral from 0 to infinity, code Integrate_myfunc(0, .). Returned will be 0.49999999999936, a result accurate to 12 digits.
If you needed a result accurate to 13 digits, you could set an absolute or relative tolerance. You could call q.setAbstol(1e-13) before calling q.integrate(). Or you could call q.setReltol(1e-13). Because the answer is 0.5 in this case, absolute and relative tolerances are about the same.

