Stata does margins. Does estimated marginal means. Does least-squares means. Does average and conditional marginal/partial effects, as derivatives or elasticities. Does average and conditional adjusted predictions. Does predictive margins. Does contrasts and pairwise comparisons of margins. Does more. Margins are statistics calculated from predictions of a previously fit model at fixed values of some covariates and averaging or otherwise integrating over the remaining covariates.
If that sounds overly technical, try this. margins answers the question, “What does my model have to say about such-and-such a group or such-and-such a person”, where such-and-such might be:
my estimation sample or another sample
a sample with the values of some covariates fixed
a sample evaluated at each level of a treatment
a population represented by a complex survey sample
someone who looks like the fifth person in my sample
someone who looks like the mean of the covariates in my sample
someone who looks like the median of the covariates in my sample
someone who looks like the 25th percentile of the covariates in my sample
someone who looks like some other statistics of the covariates in my sample
a standardized population
a balanced experimental design
any combination of the above
any comparison of the above
It answers these questions either conditionally—based on fixed values of covariates—or averaged over the observations in a sample. Any sample.
It answers these questions about any prediction or any other response you can calculate as a function of your estimated parameters—linear responses, probabilities, hazards, survival times, odds ratios, risk differences, etc.
It answers these questions in terms of the response given covariate levels or in terms of the change in the response for a change in levels, a.k.a. marginal effects.
It answers these questions providing standard errors, test statistics, and confidence intervals and those statistics can take the covariates as given or adjust for sampling, a.k.a predictive margins and survey statistics.
marginsplot can graph any of these margins or comparisons of margins.
Say that we are interested in the outcome y based on a person’s gender and packages of cigarettes smoked per day. Using Stata’s factor-variable notation, we can fit a logistic regression by typing
| y | Odds Ratio Std. Err. z P>|z| [95% Conf. Interval] | |
| sex | ||
| female | 1.86741 .9361923 1.25 0.213 .6990454 4.988549 | |
| smokes | ||
| 1 to 2 | 2.158654 1.008995 1.65 0.100 .8636059 5.395734 | |
| 2+ | 3.569982 1.947609 2.33 0.020 1.225439 10.40017 | |
| sex#smokes | ||
| female # | ||
| 1 to 2 | 1.022369 .638547 0.04 0.972 .3005851 3.477344 | |
| female#2+ | .6007973 .4570208 -0.67 0.503 .1352779 2.668265 | |
| age | 1.079942 .0103526 8.02 0.000 1.059841 1.100424 | |
| _cons | .0123407 .0073202 -7.41 0.000 .0038586 .0394686 |
The interaction between sex and smokes makes interpretation difficult. We can use margins to decipher their effects:
| Delta-method | ||
| Margin Std. Err. z P>|z| [95% Conf. Interval] | ||
| sex | ||
| male | .4549825 .0327108 13.91 0.000 .3908706 .5190945 | |
| female | .5481092 .0323836 16.93 0.000 .4846385 .6115799 | |
| smokes | ||
| 0 to 1 | .3937142 .0435627 9.04 0.000 .3083328 .4790955 | |
| 1 to 2 | .5332074 .0331231 16.10 0.000 .4682874 .5981274 | |
| 2+ | .5766632 .0500049 11.53 0.000 .4786554 .674671 |
We obtain predictive margins. If the distribution of cigarettes smoked remained the same in the population, but everyone was male, we would expect about 45% to have a positive outcome for y. If everyone were female; 55%. If instead the distribution of males and females were as observed but no one smoked, we would expect about 39% to have a positive outcome.
Is there a significant difference in the probability of a positive outcome between males and females? We can run tests after margins to find out:
We find evidence at the 5% significance level that the predictive margins differ for males and females.
How do sex and the number of cigarettes smoked interact? After fitting our logistic regression, we can obtain predictive margins for each of the levels in the interaction of these variables:
| Delta-method | ||
| Margin Std. Err. z P>|z| [95% Conf. Interval] | ||
| smokes#sex | ||
| 0 to 1 # | ||
| male | .339843 .0660779 5.14 0.000 .2103328 .4693533 | |
| 0 to 1 # | ||
| female | .4492108 .0561922 7.99 0.000 .3390761 .5593455 | |
| 1 to 2 # | ||
| male | .4754825 .0459507 10.35 0.000 .3854209 .5655442 | |
| 1 to 2 # | ||
| female | .5919691 .0473769 12.49 0.000 .4991121 .684826 | |
| 2+# male | .566515 .0677753 8.36 0.000 .4336778 .6993521 | |
| 2+#female | .5869408 .0742006 7.91 0.000 .4415103 .7323714 |
An easy way to look at this interaction is to graph it using Stata’s marginsplot.
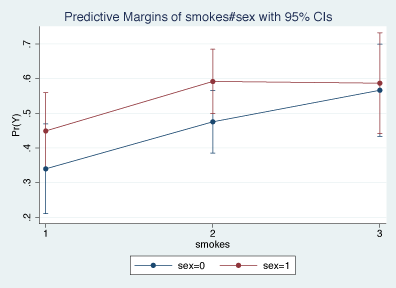
Let’s see an example of marginal effects. Because of Stata’s factor-variable features, we can get average partial and marginal effects for age even when age enters as a polynomial:
| Delta-method | ||
| dy/dx Std. Err. z P>|z| [95% Conf. Interval] | ||
| age | .0015255 .0032462 0.47 0.638 -.0048369 .0078879 |
We are using different data than before. The probability that a person is in a union increases by 0.0015 as age increases by one year. By default, margins reports average marginal (partial) effects, which means effects are calculated for each observation in the data and then averaged.
Alternatively, if we wanted effects at the average of the covariates, we could type
Stata’s margins includes options to control whether the standard errors reflect just the sampling variation of the estimated coefficients or whether they also reflect the sampling variation of the estimation sample. In the latter case, margins can account for complex survey sampling including weights, sampling units, pre- and poststratification, and subpopulations.
margins works after EVERY Stata estimation command except exact logistic and exact Poisson; alternative-specific conditional logistic, alternative-specific multinomial probit, and alternative-specific rank-ordered probit; nested logit; generalized method of moments; structural vector autoregressive models; state space; unobserved components; and structural equation models.

